Arc Intersections for a Nice Bow

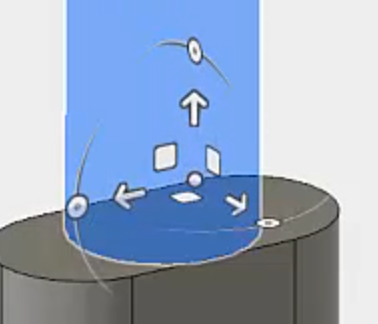
As part of rebuilding the Numsolar 3D editor to make it easier to use, I was researching rotate/scale/translate widgets. I mean the small visual tool that lets you manipulate objects:

An example from Fusion 360 How To Rotate.

This is from Fusion 360. See that nice bow shape with tapered ends? I want that!

I’m writing this blog post, because it serves as a useful example of the level of mathematics that is good to know as a general software engineer. Now, if I write 3D parametric CAD, you’re probably thinking this will be a post intersecting 3D solids, and computing bounding surfaces. But my point here is that even something as mundane as a good looking cursor can contain interesting problems that “requires maths.” Do you have to solve it mathematically this way?

Well, you would probably use a vector drawing program, export an SVG and load that as your cursor. But what if you were asked to make it configurable? Perhaps you can export to SVGs? Perhaps you can linearly extrapolate between the two. Maybe you could draw to circles and take the difference? Or we solve a bit of maths.

Tearing It Down

I use OnShape for my CAD needs, but Fusion 360 sure has more eye candy and bright colors. This widget is essentially the same 2D shape instantiated for the three axes:

The pivot point at the center.
The arrow to move along one axis.
The square to slide along a plane.
The bow and circle for rotating around the pivot.

Notably, the arrow and pivot are actually sprites that are always angled towards the camera, while the rest are stuck in their plane. This makes total intuitive sense as the arrow is the only 1D modifier and the pivot is a point. Let’s skip computing the outline and making that a contrasting color, as it is a topic for a whole other blog post.

What I’ll focus on here is the bow, which tapers off so nicely at the ends. It’s really the difference between two circle sectors of different diameters, slightly offset. Looks more like a video game than a CAD tool, and it’s great. We can reproduce that in Three.js, but how do we find the arc coordinates to do so?

Modelling

The first question is: which parameters could we be dealing with? For this, we’ll note it doesn’t matter which direction the circles are offset. We’ll use the x-axis. And they are symmetric around the x-axis, so we’ll only care about the first quadrant.

Two diameters or radii
The distance from circle centers to intersection
Two angles to the point of intersection; one for each circle (since they different centers)
An offset between the circles along the axis
The x and y-coordinates of the intersection, from each circle center
The maximum thickness of the bow, which is the difference of where each arc intersects the axis

That’s ten parameters. We’ll immediately note the diameter and distance to intersection must be the same, so really eight. Which ones are inputs, and which do we want to compute?

What I care about visually is the length of the bow, and the thickness. So to me, it makes sense that one of the angles and the thickness should be inputs. What do we need for outputs?

To draw arcs with Path.arc, we need the center coordinates, radius and start/end angles:

Path.arc(x, y, radius, startAngle, endAngle, clockwise)

The first center is arbitrary (let’s say the origin,) and the second center is at a small offset. Can we compute the rest from the two inputs, or do we have to make more assumptions?

Intermezzo

My dad told me about a mathematics school teacher who was confronted with this question from a pupil:

Why do I need to learn this!? I’m going to be laying bricks!

Of all the questions in mathematics, the “why” is probably the most difficult to answer. It’s just so personal. Mathematics is just a tool to explain the world, and to communicate it to others. Whether it’s a tool you need depends on what you want to accomplish. Like, I haven’t learned to use a dosimeter. Why? Because if I am ever in a situation where I need to care about radiation levels, exact measurement is probably the least of my concerns. I’ll stick to “if it beeps annoyingly, I’ll run” for now.

The teacher responded with

You arrive at the job site, and are given drawings of the width, height and depth of the wall. How many bricks and how much mortar do you have to buy?

You don’t need to learn everything about mathematics to make it useful. No one simply “knows maths.” But tools are useful to be aware of.

Finding a Solution

The first order of business is to invent some names:

Names for the model.

To set up the equation system, we need to think about what relationships are the same, expressed in more than one way. The easiest to me is that the y-coordinate of the intersection must be the same for the two circles. The x-coordinates are the same, except with the added offset. That leads to

$$ \left\{\begin{array}{ll} R \sin \alpha &= r \sin \beta \\ R \cos \alpha &= r \cos \beta + d \\ R + t &= r + d \end{array}\right.\tag{1} $$

where $R$ and $r$ are the radii, $\alpha$ and $\beta$ are the intersection angles, for the respective circles, $d$ is the distance between the circle centers and $t$ is the bow thickness.

With a bit of thought into what happens for really small and large circles, we realize that the larger diameter circle must be the inner arc of the bow. This suggests $R$ and $\alpha$ is our origin circle, since that makes $d$ positive. Thus, we want to solve for $r$, $\beta$ and $d$. Luckily, that means we have three equations and three unknown. Using the trigonometric identity, we turn this into

$$ \left\{\begin{array}{ll} R + t - r &= R \cos \alpha - r \sqrt{1 - \left(\frac{R}{r}\right)^2 \sin^2 \alpha} \\ \sin \beta &= \frac{R}{r} \sin \alpha \\ d &= R - r + t \end{array}\right.\tag{2} $$

Of course, the top one is annoying, and the others are fine. Rearranging to solve for $r$, and squaring, the second degree term actually vanishes and we’re left with a unique-ish solution. We only care about intersections in the first quadrant, and I’m pretty sure the solution we’re discarding due to the squaring is in the second quadrant.

$$ \left\{\begin{array}{ll} r &= \frac{R^2 \sin^2 \alpha + (R(1 - \cos \alpha) + t)^2}{2(R(1 - \cos \alpha) + t)} = \frac{R^2 \sin^2 \alpha + k^2}{2k} \\ k &= R(1 - \cos \alpha) + t \\ \sin \beta &= \frac{R}{r} \sin \alpha \\ d &= R - r - t \\ \end{array}\right.\tag{3} $$

where I introduced $k$ to reduce clutter.

And there we have all unknown expressed only in terms of known (if you read them in order.)

Coding the Solution

So how do we code this up?

All the pieces are there, so let’s just write some code that outputs an SVG:

An interactive example with Preact generating an SVG.

If you take $\alpha$ all the way towards 85°, it will shift out of place. This is the SVG sweep parameter that needs to be flipped. The same thing happens if you increase thickness beyond about 0.4. That’s the long-arc paramter that needs flipping. Both are left as an exercise for the reader.